こんにちは!
今回は、暗算のスピードに悩んでいる人向けに、計算テクニックをご紹介します!
フェルミ推定の時などに活用いただければと思います。
以前、「フェルミ推定などでよく使う数字の記事」を書いたので、そちらと合わせてご利用ください!

一番重要な “対数計算”
皆さん、高校時代にlogとかを勉強されましたよね?
どこで使うんだよあんなの
という感想を持った人は多いと思います(私もそうでした)。
しかし、むしろ対数計算は、ビジネスや政策立案の現場で一番使うんじゃないかと思います。
コンセプトは、「桁数は、桁数だけ取り出して計算する」ということです。
例えば、
50万円 × 12万円 = ?
を皆さんどうやって計算しますか?
コツは、対数の部分と、有効数字の部分を分けて計算することです。
今回の場合は、
- 対数の計算:1万 × 1万 = 1億
- 有効数字の計算:50 × 12 = 600
なので、
50万円 × 12万円 = 600億円
となります。
この対数計算を覚えると、一気に計算が早くなりますので、ぜひ参考にしていただければ!
特に覚えておきたいのはこちらです!
- 万 × 万 = 億
- 万 × 億 = 兆
- 億 × 億 = 京
- T(千) × T(千) = M(100万)
- T(千) × M(100万) = B(10億)
- T(千) × B(10億) = Tr(1兆)
- M(100万) × M(100万) = Tr(1兆)
- 兆 ÷ 万 = 億
- 兆 ÷ 億 = 万
- 億 ÷ 万 = 万
- Tr(1兆) ÷ B(10億) = T(千)
- Tr(1兆) ÷ M(100万) = M(100万)
- Tr(1兆) ÷ T(千) = B(10億)
- B(10億) ÷ M(100万) = T(千)
- B(10億) ÷ T(千) = M(100万)
- M(100万) ÷ T(千) = T(千)
数値を分解して計算する
算数で習った「分配法則」もよく用います。
例えば、
17 – 0.99 = ?
のときは、「– 0.99」の部分を「- 1 + 0.1」と分解し、
17 – 1 + 0.1 = ?
とした方が計算が早いです。
まずは基準値を計算して、その後調整する
10や0.1など、簡単に暗算できる数字を基準値として計算して、それを調整する計算方法です。
例えば
52 × 0.3 = ?
のときは、まずは
52 × 0.1 = ?
を計算し、その後に
× 3
とすると、暗算が簡単になります。
かけ算を頭からやる
かけ算は、筆算では下の段からやるので、暗算が苦手な人が多い印象です。
頭からかけ算をやるやり方を覚えると、計算が早くなります
例えば、
23 × 54 = ?
というとき、まずは頭から計算ということで、
23 × 50 = ?
を計算し、次に
23 × 4 = ?
を計算し、最後に両方を足し合わせれば、早く暗算できます。
ここで、
23 × 50 = ?
の部分は、上記の「まずは基準値を計算して、その後調整する」を使って、
23 × 10 × 5 = ?
としましょう。
また、冒頭の「一番重要な “対数計算”」における「50 × 12 = ?」部分についても、
50 × 10 + 50 × 2 = ?
と頭から計算を意識した方が早いです。
割り算も頭からやる
割り算も頭からやることを意識すると早くなります。
例えば、
78 ÷ 3 = ?
は、まずは頭から
7 ÷ 3 = 2 あまり1
とし、この「あまり1」は、10なので、残りは18。
なので、
18 ÷ 3 = 6
となり、2と6を組み合わせて、
78 ÷ 3 = 26
とした方が早いです。
割り算は、分母と分子に同じ数字をかけ算する
他の割り算のテクニックとしては、分母と分子に同じ数字をかけても答えは変わらないという性質を使い、簡単な式に変換するというものがあります。
例えば、
65 ÷ 5 = ?
は、分母を10にしたら計算が楽なので、分母と分子に2をかけて、
130 ÷ 10 = ?
とすると計算が楽です
また、例えば
450 ÷ 25 = ?
については、分母を100にしたら計算が楽なので、分母と分子に4をかけて、
1800 ÷ 100 = ?
とすると、計算が楽です
さらに応用として、
「先に分母か分子のいずれからに数字をかけて、最後にもう片方(分母か分子)に同じ数字をかける」
というものもあります。
例えば、
650 ÷ 1.1 = ?
のとき、少数計算が嫌なので、まずは分母に10をかけます。
すると、
650 ÷ 11 = ?
となり、割り算は頭から計算すればいいので、この時の答えば
650 ÷ 11 = 59.09・・・
となるのが分かります。
ここに、分子にかけるはずだった10をかけると、
650 ÷ 1.1 = 650 ÷ 11 × 10 = 590.9・・・
となります。
二桁の計算:両方とも十の位が1だった時
二桁の計算において、両方とも十の位が1だった時、「焼肉じゅうじゅう方式」という計算方法が使えます。
「ためしてガッテン」で紹介されていた計算方法らしいです。
流れとしては、
- 片方の数字と、もう片方の数字の”一の位”を足して、10をかける
- 片方の数字の”一の位”と、もう片方の数字の ”一の位”をかける
- 上記の式から計算された2つ数字をたす
という形になります。
例えば、
17 × 15 = ?
のときは、以下のようになります。
二桁の計算:2乗の時
2乗の時も、テクニックがあります。
流れとしては、
- 片方の数字と、もう片方の数字の”一の位”を足して、両方の”十の位”をかける
- 両方の”一の位” をかける
- 上記の式から計算された2つ数字をたす
という形になります。
例えば、
32 × 32 = ?
のときは、以下のようになります。
2桁の計算:「二桁 × 2乗」の応用
以下の考え方で「二桁 × 2乗」を応用すると、一気に適用範囲が広がります。
はじめてこの考え方を先輩に聞いた時は、
すげー!
と感動しました。
考え方としては、二桁の計算を、「二桁 × 2乗」の計算に変換します。
例えば、
26 × 22 = ?
のときは、
(24 + 2) × (24 – 2) = ?
と変形します。
すると、
(24 + 2) × (24 – 2) = 24^2 – 2^2 = ?
と、2乗の計算に変換できますので、あとは「二桁 × 2乗」を使って計算すればOKです!
よくある加重平均の計算式
フェルミ推定などをするときは、比率の計算などで加重平均をよく使います。
ここで、加重平均の計算をささっと終わらせるために、よく出てくる加重平均のウェイト値(=各象限の確率)は暗記しておくことが重要です。
一例として、「平日か休日か」によって切り分けるパターンを考えてみましょう。
飲食店やマッサージなどの小売・サービス業では、平日か休日かによって数字が変わる時が多いので、よく使う式です。
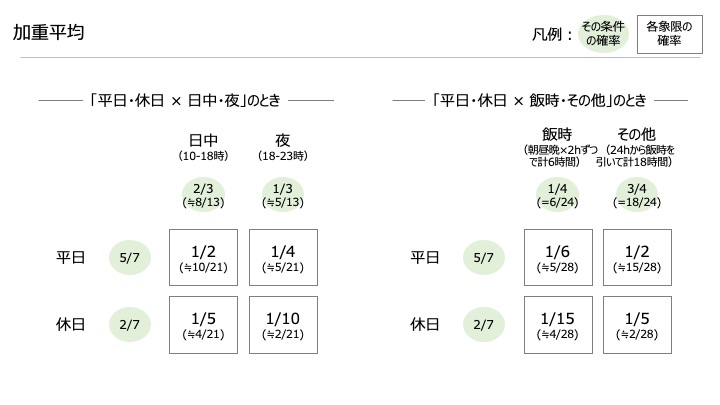
その他覚えておいた方がいいもの
8の段の分数は、覚えておくと何かと便利です!
- 1/8 = 0.125
- 3/8 = 0.375
- 5/8 = 0.625
- 7/8 = 0.875
おわりに
今回は以上です!
お仕事に参考にしていただければ幸いです。








